Ronan Memin's webpage

About me

I am a post doctoral researcher at IMT (Toulouse) in the probability team with Michel Pain. Starting October 2025, I will be part of the Statistical Physics and Mathematics program as a post doctoral researcher at DMA (ENS, Paris).

My research focuses on random matrix theory and its interactions with integrable systems, and more generally, I am interested in the study of random matrices through large deviations for the spectrum/the largest eigenvalue, fluctuations/local statistics of the spectrum.

I have completed my PhD thesis under the supervision of Alice Guionnet (ENS Lyon) in September 2023. You can find my CV here.

Contact

You can reach me at ronan.memin[at]math.univ-toulouse.fr.

Research papers

• Large deviations at the edge for 1D gases and tridiagonal random matrices at high temperature, with Charlie Dworaczek Guera [arXiv preprint]
• CLT for real beta-ensembles at high temperature, with Charlie Dworaczek Guera [Electronic Journal of Probability, link]
• CLT for beta ensembles at high temperature, and for integrable systems : a transfer operator approach, with Guido Mazzuca [Annales de l'Institut Henri Poincaré, link]
• Large deviations for the Ablowitz-Ladik lattice, and the Schur flow, with Guido Mazzuca [Electronic Journal of Probability, link]
• Large deviations for generalized Gibbs ensembles of the classical Toda chain, with Alice Guionnet [Electronic Journal of Probability, link]

PhD thesis

You can access my PhD thesis Analysis of certain integrable models via random matrix theory here. The key objects at stake are the following:

- discrete space integrable systems, such as the Toda chain, or the Ablowitz-Ladik lattice, whose dynamic can be encoded by the evolution of a Lax pair, which is a pair of N by N matrices.

- the beta ensembles of random matrix theory, which are the law of the spectrum of particular instances of random matrices. The real beta ensemble is the probability measure on R^N given, for any beta > 0 and V going fast enough to infinity, by

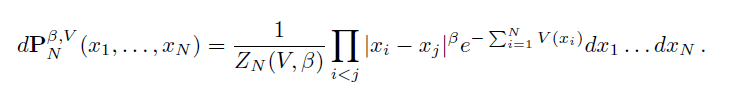
Here, we are interested in the high temperature regime, which is the regime where beta is proportional to 1/N.

Motivated by the derivation of a hydrodynamic limit for integrable systems, Herbert Spohn uses a comparison between integrable systems and the beta-ensembles at high temperature. We strenghten the understanding of this link through a large deviations approach for the empirical measure of eigenvalues of the matrices of interest, and through the study of the fluctuations of those measures.

Last update of the website: 29 Jul. 2025