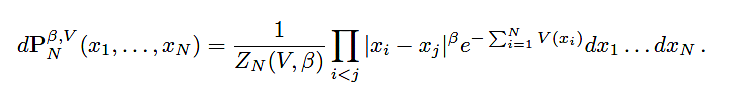
You can access my PhD thesis (under the direction of Alice Guionnet) Analysis of certain integrable models via random matrix theory here. The key objects at stake are the following:

- discrete space integrable systems, such as the Toda chain, or the Ablowitz-Ladik lattice, whose dynamic can be encoded by the evolution of a Lax pair, which is a pair of N by N matrices.

- the beta ensembles of random matrix theory, which are the law of the spectrum of particular instances of random matrices. The real beta ensemble is the probability measure on R^N given, for any beta > 0 and V going fast enough to infinity, by

Here, we are interested in the high temperature regime, which is the regime where beta is proportional to 1/N.

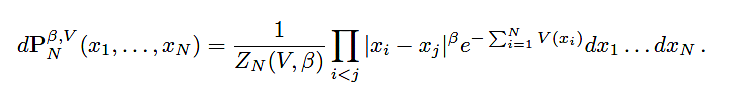
Motivated by the derivation of a hydrodynamic limit for integrable systems, Herbert Spohn recently used a comparison between integrable systems and the beta-ensembles at high temperature. We strenghten the understanding of this link through a large deviations approach for the empirical measure of eigenvalues of the matrices of interest, and through the study of the fluctuations of those measures.

back to main page